Primoridal Black Holes and Induced Gravitational Waves with Logarithmic Non-Gaussianities
Summary
Primordial Black Holes (PBHs) are a powerful probe of the early Universe, offering an opportunity to investigate, and provide constraint, on various models of the early universe. In the standard PBH formation channel, rare large curvature perturbations generated during inflation, collapse after re-entering the Hubble domain during the radiation domination epoch before the Big Bang Nucleosynthesis. Importantly, these large perturbations can source both PBHs and a background of scalar-induced gravitational waves (SIGWs), which are now within reach of pulsar timing array (PTA) experiments.
In our recent paper arXiv:2411.07647, we investigate PBH formation and the associated SIGW signal for a class of models characterised by their intrinsic local non-Gaussianities (NG) effects. We exploit the logarithmic duality relation which links the nature of a non-Gaussian parameter $\gamma$ with the profile shape of the curvature perturbations $\zeta(r)$ and its probability distribution function (PDF). Thus, the importance of non-Gaussianity is two-fold: 1) it modifies the tail of PDF, of which the PBH abundances is exponentially sensitive, and 2) it modifies the shape of the the curvature perturbation, which affects the amplitude threshold required to form a PBH.
The PDF and curvature profile as functions of the NG parameter $\gamma$ are given as follows:
\[P(\zeta) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left[ - \frac{1}{2 \gamma^2 \sigma^2} \left( e^{-\gamma \zeta} - 1 \right)^2 - \gamma \zeta \right]\]and
\[\zeta (r; \mu,\, \gamma) = -\frac 1\gamma \ln \left[ 1 - \gamma \zeta_G(r; \mu) \right] , \qquad \rm{with} ~ ~ \zeta_G(r; \mu) = \mu\, \rm{sinc} (k\,r)\]Roughly speaking, large positive NGs with $\gamma >0$ have a heavier tail in the PDF distribution, and the shape profile of $\zeta(r)$ becomes more peakier around it’s origin, what reduces the required amplitude threshold $\mu_c$. The addition of these two effects results into the enhancement of PBH formation. On the contrary, large negative NGs with $\gamma < 0$ yield a suppressed tail in the PDF, (leading to a Gumbel distribution), and the curvature profile shapes become wider reassembling a plateau around the radial origin. This has interesting effects as it shifts the Laplacian away from the centre of the perturbation adding complexity in the Ricci curvature (to be described in future entries of this blog). The add-up of these effects, yields to a decrease on the PBH abundances, however this might revert for very strong negative NGs as a consequence of the decreasing collapse thresholds for $\gamma \lesssim -3.1$.
The methodology of these work is as follows: 1) We compute the collapse thresholds $\mu_c$ using full Numerical Relativity simulations. 2) We compute the PBH abundances assuming a monochromatic power spectrum at $k_\star$ with amplitude $A_G$. Then, we fix the value of $A_G$ to the limit where all the dark-matter corresponds to PBHs ($ f_{\rm PBH}^{\rm tot} =1$). Figure 1 shoes the variation of the collapse thresholds with respect the NG-parameter $\gamma$, and the mass distribution functions (for the case when $ f_{\rm PBH}^{\rm tot} =1 $).
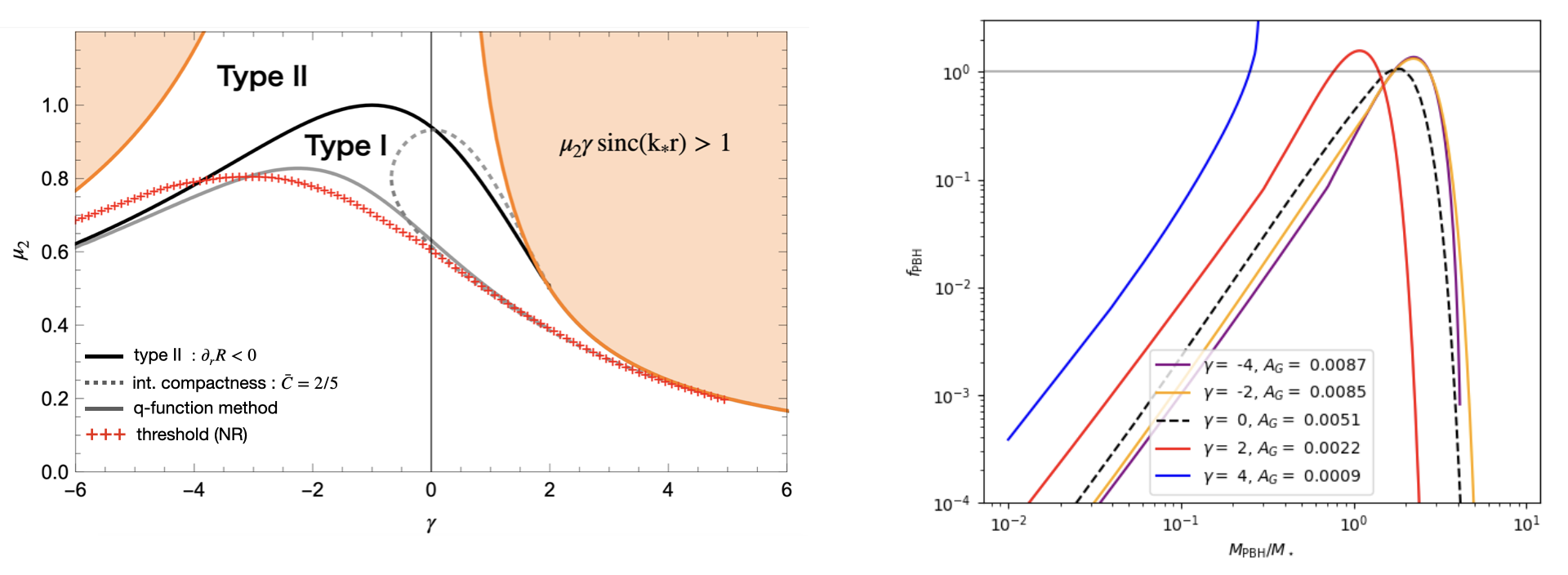
Fig. 1 Left: Thresholds for PBH formation with respect the NG parameter $\gamma$. Right: PBH mass function after imposing $f_{\rm PBH} = 1$.
Gravitational Signatures
Once we know the power spectrum, we compute the SIGWs associated to it, taking into account the NG effects, by computing
\[\Omega_{\rm GW} = \frac 1{48} \sum_{\lambda,\lambda' } { \overline { {\cal P}_{\lambda \lambda'} }} \propto \langle hh \rangle\]where
\[\langle hh \rangle \propto \langle \zeta_G\zeta_G\zeta_G\zeta_G \rangle + f_{\rm NL} \langle \zeta_G\zeta_G\zeta_G^2\zeta_G^2 \rangle + g_{\rm NL} \langle \zeta_G\zeta_G\zeta_G\zeta_G^3\rangle \\ \qquad + f_{\rm NL}^4 \langle \zeta_G^2\zeta_G^2\zeta_G^2\zeta_G^2 \rangle + f_{\rm NL}^2 g_{\rm NL}^2 \langle \zeta_G\zeta_G^2\zeta_G^2\zeta_G^3\rangle + ... {\cal O}(A_G^4)\]Finally, we provide the predicted SIGWs for these class of models in the frequency band of LISA (the mHz band), and we perform a Bayesian parameters estimation regarding the PTA signal (in the nHz band), as shown in Figure 2.
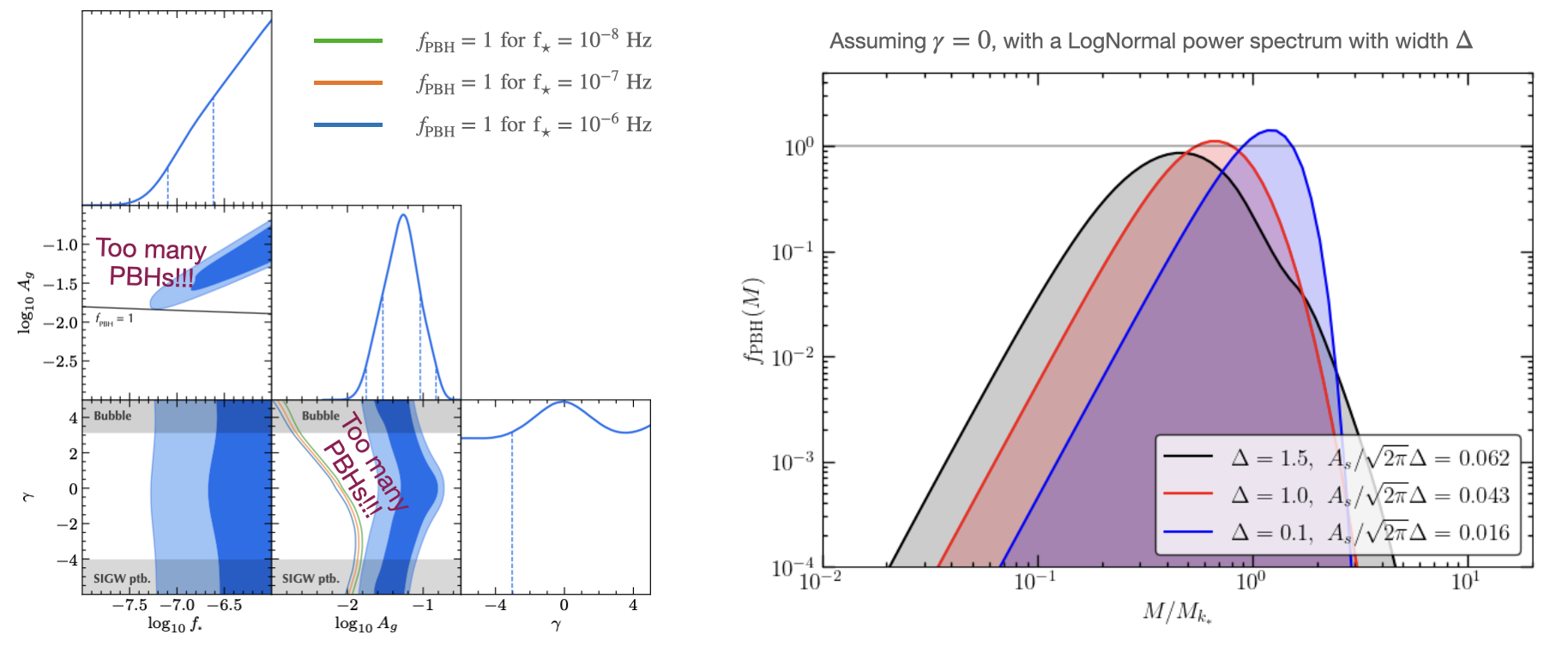
Fig. 1 Left: Thresholds for PBH formation with respect the NG parameter $\gamma ~.$ Right: PBH mass function after imposing $f_{\rm PBH}^{\rm tot} = 1$.
Ending note
As a conclusion, we show that the PTA signal is incompatible with SIGWs from PBHs under the assumption of a monochromatic power spectrum. However, we will soon show, that relaxing this condition by allowing a finite width peak in the power spectrum (e.g. with a Log-Normal shape), the PTA data can be easily accommodated to the expected signal from PBH models producing planetary-mass black holes…
If interested, stay tuned for the next update!
References:
- Inui, R., Joana, C. Motohashi, H., Pi, S., Tada, Y., Yokoyama, S., ``Primordial black holes and induced gravitational waves from logarithmic non-Gaussianity”, J. Cosmol. Astropart. Phys. 2025 021, arXiv:2411.07647
